阅读 xtq 的 2023 年集训队论文《一类基础子串数据结构》,对它进行一个摘抄和注解。
主要在原论文的基础上,增加了一些思路的解释和图片,试图将其变得更容易阅读。例题则补充了一道新近的题目。
第一次在 UOJ 上发东西,好紧张啊
为什么引用内的字体比正文字体大几个字号啊???
进度:最后一个“树链剖分”部分还在咕咕施工中。
1 前言
摘抄自 xtq 的论文:
字符串理论已在 OI 发展很久,其中逐渐产生了 SA、SAM 等高级后缀数据结构。这些结构深入剖析了字符串的性质,可以用来高效地解决大量的字符串问题。而这些后缀数据结构大多为单向联系,仅能处理后缀关系,而无法同时处理与前缀关系相关的内容。由此,笔者借助 SDOI2022 子串统计这道题目,对一类能够同时处理前后缀的字符串结构展开了研究,并写作了本文。该结构在此前从未出现过,所以笔者将其命名为基本子串结构。
简单来说就是:一众后缀结构处理后缀关系很强,处理前缀关系很菜。我们把两个后缀结构拼在一起,就可以得到处理两个方向都很强的结构。这就是基本子串结构的最基本思路。
2 约定与记号
字符集和字符串
默认 $|\Sigma|=O(1)$。
用 $|s|$ 表示有限字符串 $s$ 的长度,即其包含的字符的数量。
子串
对于长度为 $n$ 的字符串 $s=s_1s_2s_3\dots s_n$,用 $s[l,r]$ 表示 $s_ls_{l+1}s_{l+2}\dots s_r$ 这个子串。一般认为 $1\le l\le r\le n$。
子串中有“前缀”和“后缀”这两种特殊子串。不考虑空前缀和空后缀,其余不再赘述。
非空字符串 $t$ 是字符串 $s$ 的子串,当且仅当存在 $(l,r)$ 使得 $s[l,r]=t$。反过来,若 $t$ 是 $s$ 的子串,则可以说“$s$ 包含 $t$”。
occurence
对于字符串 $s$ 及其任意一个子串 $t$,用 $\operatorname{occ}_s(t)$ 表示 $t$ 在 $s$ 中的出现次数,也就是满足 $s[l,r]=t$ 的 $(l,r)$ 对的对数。每个这样的 $s[l,r]$ 称为 $t$ 的一个出现位置。
后缀树
$T_0$ 为正串 SAM 的 parent 树,也即反串的后缀树。
$T_1$ 为反串 SAM 的 parent 树,也即正串的后缀树。
默认 $T_0$ 与 $T_1$ 上的结点等价于其对应 SAM 上的对应结点。
border
称 $s$ 的子串 $t$ 为 $s$ 的 border,当且仅当 $t$ 既是 $s$ 的前缀,又是 $s$ 的后缀,也即 $s[1,|t|]=s[|s|-|t|+1,|s|]=t$。
3 基本子串结构
3.1 引入
让我们从一道例题开始:
例题 3.1.1
给定字符串 $s$,$q$ 次询问 $T_0$ 和 $T_1$ 中指定的两个结点代表的字符串的交集。
目标复杂度为 $O(|s|+|q|)$。
很明显,这道题需要我们将正反串的 parent 树(或者说是后缀树)合起来考虑。根据这个思路,我们就可以逐步得到基本子串结构。
3.2 结构
$T_0$ 和 $T_1$ 上的结点代表的字符串都有特别的结构。$T_0$ 中一个结点代表的字符串两两互为后缀,且 $\operatorname{occ}$ 相同;$T_1$ 中一个结点代表的字符串两两互为前缀,且 $\operatorname{occ}$ 也相同。想要把它们联系起来,我们就需要从此入手。
以下默认 $s$ 是一个固定的字符串(母串)。$\operatorname{occ}$ 若无特殊说明,则指代 $\operatorname{occ}_s$。
某些比较简单的证明和比较直观易懂的内容的证明将不会保留。
扩展串及其性质
我们引出以下概念:
定义 3.1(扩展串)
对于字符串 $s$ 的一个子串 $t$,定义其扩展串 $\operatorname{ext}(t)$ 为最长的 $s$ 的子串 $t'$,使得其满足 $t$ 为 $t'$ 的子串且 $\operatorname{occ}(t')=\operatorname{occ}(t)$。
首先解决它的良定问题:
引理 3.2.1
对于 $s$ 的子串 $t_1$ 和 $t_2$,若 $t_1$ 包含 $t_2$,则 $\operatorname{occ}(t_1)\le \operatorname{occ}(t_2)$。
引理 3.2.2
对于一个子串 $t$,$\operatorname{ext}(t)$ 存在且唯一。
证明
存在性不必多说,$t$ 本身便满足条件。
考虑唯一性。反证法,设存在两个不同的字符串 $t_1$ 和 $t_2$ 符合扩展串条件。
因为 $\operatorname{occ}(t)=\operatorname{occ}(t_1)=\operatorname{occ}(t_2)$,且 $t$ 为 $t_1,t_2$ 的子串,所以 $t$ 的出现和 $t_1,t_2$ 的出现一一对应。
考察 $t$ 在 $s[l,r]$ 的一次出现。我们可以找到 $(l_1,r_1)$ 满足 $s[l_1,r_1]=t_1$ 且 $l_1\le l\le r\le r_1$;对于 $t_2$ 可以找到同样的 $(l_2,r_2)$。在此,不妨假设 $r_1
注意到,由于 $l_1\le l_2\le r_1\le r_2$,故可以验证子串 $t'=s[l_1,r_2]$ 也满足“$t$ 是 $t'$ 的子串”和“$\operatorname{occ}(t)=\operatorname{occ}(t')$”,但是 $|t'|>|t_1|=|t_2|$,所以 $t_1,t_2$ 不可能为 $t$ 的扩展串,矛盾。
由这个证明过程,我们得到两个推论:
推论 3.2.1
对于子串 $t$ 和 $t'=\operatorname{ext}(t)$,若 $s[l,r]=t,s[l',r']=t'$ 且 $l'\le l\le r\le r'$,则对于任意的 $l'\le l''\le l\le r\le r''\le r'$,都有 $\operatorname{ext}(s[l'',r''])=t'$。
推论 3.2.2
对于子串 $t$,$\operatorname{ext}(\operatorname{ext}(t))=\operatorname{ext}(t)$。
等价类
parent 树上其实也有类似的“扩展串”结构,只不过它们的“扩展串”严格要求原串为其前缀或后缀。之后,“扩展串”就将 $s$ 的子串划分进了若干个结点(即等价类)中。在此,我们做同样的动作。
定义 3.2(等价关系)
对于子串 $x,y$,两个串之间等价当且仅当 $\operatorname{ext}(x)=\operatorname{ext}(y)$。
容易验证该关系的自反性、对称性和传递性。要精确一点的话,这样才能称其为“等价关系”,直接将它命名为“等价关系”不太合理。
根据等价关系,$s$ 的子串自然地被划分为了若干个等价类。我们取出每个等价类中具有代表性的元素:
定义 3.3(代表元)
对于子串 $t$,若 $\operatorname{ext}(t)=t$,则称 $t$ 为 $t$ 所在等价类的代表元。
若 $t$ 所属的等价类为 $g$,则用 $\operatorname{rep}(g)=t$ 表示 $g$ 的代表元。
引理 3.2.3
对于每个等价类 $g$,$\operatorname{rep}(g)$ 存在且唯一。
引理 3.2.4
对于子串 $t_1,t_2$,若 $\operatorname{occ}(t_1)=\operatorname{occ}(t_2)$ 且 $t_1$ 包含 $t_2$,则 $t_1$ 与 $t_2$ 等价。
等价类的直观结构
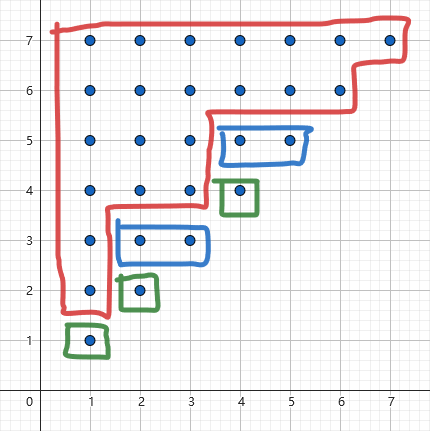
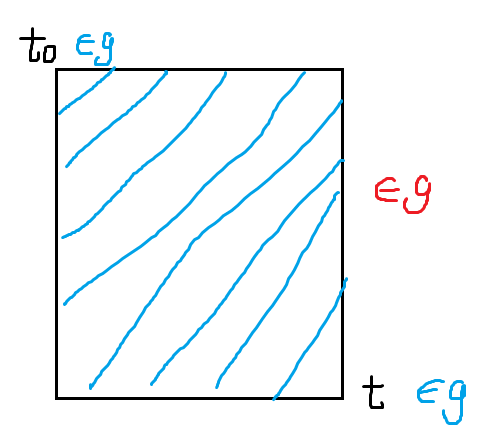
仅仅这样划分等价类还不够。parent 树的等价类的内部结构是很清晰的,但是现在的这个等价类内部还是很乱。怎么将它们排列好?考虑到子串可以和区间对应,我们引入平面直角坐标系上的点来代表子串。
注 因为绘图时格子比较好画,所以手绘的示意图中也会用方格表示子串。
定义 3.4(first occurence)
对于子串 $t$,定义 $\operatorname{posl}(t)=\min\{l:s[l,l+|t|-1]=t\},\operatorname{posr}(t)=\min\{r:s[r-|t|+1,r]=t\}$。
用 $\operatorname{posl}$ 和 $\operatorname{posr}$,我们为每一个子串确定了一个出现位置。现在结合前面的引理,我们可以得到基本子串结构的关键性质:
定理 3.1(阶梯状结构)
建立以 $l$ 为横轴,$r$ 为纵轴的平面直角坐标系,子串 $t$ 对应于点 $(\operatorname{posl}(t),\operatorname{posr}(t))$。
则,每个等价类内的子串在平面上对应的点构成了一个上侧和左侧对齐,下侧和右侧呈阶梯性的阶梯状点阵。
证明
取一等价类 $g$,设 $t_0=\operatorname{rep}(g)$,再设 $(l_0,r_0)=(\operatorname{posl}(t_0),\operatorname{posr}(t_0))$。
考虑 $g$ 中任意字符串 $t$,它对应于点 $(l,r)=(\operatorname{posl}(t),\operatorname{posr}(t))$。根据 $\operatorname{ext},\operatorname{posl},\operatorname{posr}$ 的定义,有 $l_0\le l\le r\le r_0$。再根据引理 3.2.1,可知所有 $l_0\le l'\le l\le r\le r'\le r_0$ 的串 $t'=s[l',r']$ 都在 $g$ 中。在平面上,这些串对应的就是以 $(l_0,r_0)$ 为左上角、以 $(l,r)$ 为右下角的所有点。该定理即得证。
Fig 3.1 矩形点阵 推论 3.2.3
所有 $1\le l\le r\le |s|$ 的点被等价类划分为了若干个互不相交的阶梯形。其中,等价类 $g$ 对应的阶梯形出现了 $\operatorname{occ}(\operatorname{rep}(g))$ 次。
定义 3.5(周长)
对于一个等价类 $g$,其周长 $\operatorname{per}(g)$ 为其对应的阶梯状点阵的行数和列数之和。
为了让这个性质更加易懂,在此略举一例。
假设 $s=\texttt{aababcd}$,那么可以划分为如下几个等价类:
$$ \begin{aligned} {\color{red}{g_1}}=&\{\texttt{aa},\texttt{aab},\texttt{aaba},\texttt{aabab},\texttt{aababc},\texttt{aababcd}\}\cup\\ &\{\texttt{aba},\texttt{abab},\texttt{ababc},\texttt{ababcd}\}\cup\\ &\{\texttt{ba},\texttt{bab},\texttt{babc},\texttt{babcd}\}\cup\\ &\{\texttt{abc},\texttt{abcd}\}\cup\\ &\{\texttt{bc},\texttt{bcd}\}\cup\\ &\{\texttt{c},\texttt{cd}\}\cup\{\texttt{d}\}\\ {\color{blue}{g_2}}=&\{\texttt{b},\texttt{ab}\}\\ {\color{green}{g_3}}=&\{\texttt{a}\} \end{aligned} $$
对应到平面上,阶梯状图形就是:
等价类和后缀树
等价类的直观结构已经很漂亮了,但我们还可以进一步将它和后缀树联系在一起。
此处再提醒一次:$T_0$ 为正串 parent 树/反串后缀树,$T_1$ 为反串 parent 树/正串后缀树。
$T_0$ 中一个结点代表的字符串两两间存在后缀关系,且 $\operatorname{occ}$ 相同。放到平面上考虑,这相当是说 $T_0$ 中一个结点代表的字符串同属于一个等价类,且在该等价类的阶梯状点阵中处于同一行。类似地,$T_1$ 中一个结点代表的字符串就该处于同一列。进一步地,我们可以得到:
定理 3.2(等价类和后缀树结点的对应)
对于任意等价类,其阶梯状点阵中,每一行对应 $T_0$ 中的一个结点,每一列对应 $T_1$ 中的一个结点,且所有等价类中的所有行(所有列)和 $T_0$($T_1$)中的所有结点形成一一对应的关系。
“对应”指“包含的字符串集合相同”。
证明
口胡了口胡了以行和 $T_0$ 结点之间的对应关系为例。设等价类行集合为 $R$,$T_0$ 结点集合为 $V$。设 $c\in R$ 包含的字符串为 $S(c)$;$u\in V$ 表示的字符串为 $T_0(u)$。
因为一个阶梯状点阵中同一行的字符串右端点相同,$\operatorname{occ}$ 也相同,所以对于 $c\in R$,一定存在 $u\in V$ 使得 $S(c)\subseteq T_0(u)$。因为 $\{T_0(u):u\in V\}$ 构成一个本质不同子串的划分,所以一个 $c$ 会对应到唯一的 $u$。这个映射记作 $f:R\rightarrow V$。
因为 $\operatorname{occ}$ 相同,且表示的字符串两两间有后缀关系,所以对于任意的 $u\in V$,一定存在 $c\in R$ 使得 $T_0(u)\subseteq S(c)$。因为 $\{S(c):c\in R\}$ 构成一个本质不同子串的划分,所以一个 $u$ 会对应到唯一的 $c$。这个映射记作 $g:V\rightarrow R$。
容易说明 $g(f(c))=c,f(g(u))=u$,故会形成一一对应的关系。
按 虽然在原文的定理 3.2中,作者正确地说明了“$T_0$ 结点对应行、$T_1$ 结点对应列”,但是在证明及后续讨论中,他貌似认为“$T_0$ 结点对应列、$T_1$ 结点对应行”,也就是说反了。
这样的对应关系同时也说明了另一个性质:
定理 3.3
$\sum_g \operatorname{per}(g)=O(n)$。
最后将树边连到等价类的行/列上,我们就得到了完整的基本子串结构了!
这个也很简单。对于 $T_0$ 中的树边,我们规定其方向为“从父亲到儿子”,这样一条树边就应该从一行的左边界连向另一行右边界;对于 $T_1$ 中的树边,则应该是从一列的上边界连向另一列的下边界。
按照这种连边方式,我们还可以给基本子串结构构造另一种含义:基本子串结构是一个以本质不同子串为结点的 DAG,其中 $t$ 连向 $t+c$ 和 $c+t$($t$ 为一个子串,$c$ 为一个字符)。
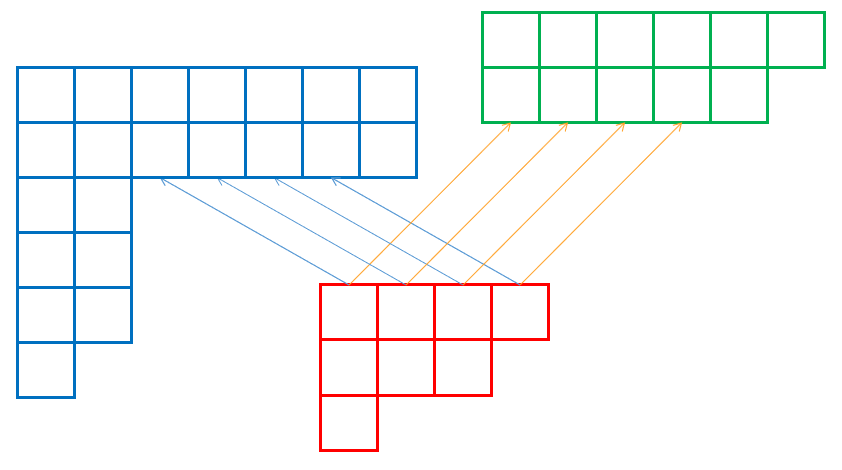
仍然以 $s=\texttt{aababcd}$ 为例,这里我们考虑它的行的连边。首先可以观察 $s$ 的正串的 parent 树,也就是 $T_0$:
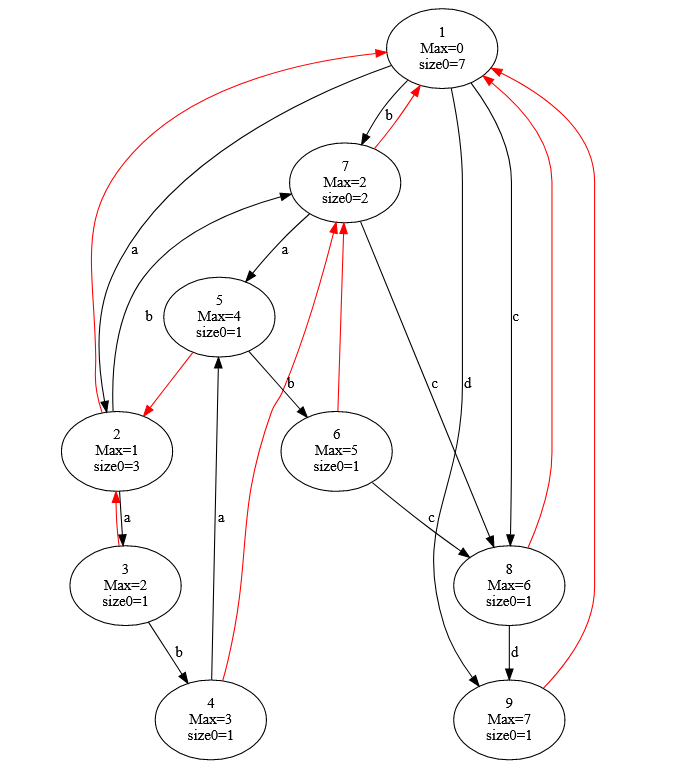
根据上面的叙述,不难得到 $T_0$ 上结点和等价类行的对应关系,连边如下:
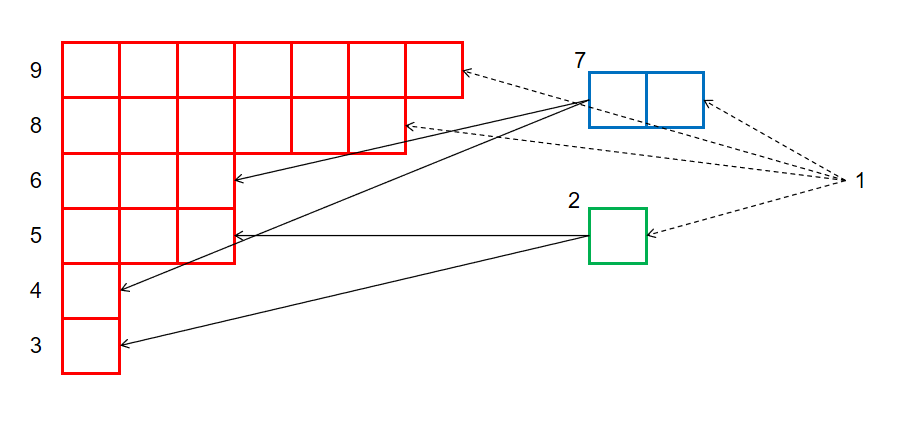
注意,在基本子串结构中,表示空字符串的根节点 $1$ 是找不到对应的,所以此处用虚线表示连向 $1$ 的父边。
从另一个角度来说,根据基本子串结构的含义和 $T_0$ 上边的含义,我们发现 $T_0$ 的树边其实就是等价类中每一行向其左边界紧邻的行连边。例如,平面上 $7$ 结点左边紧邻的结点有 $6$ 和 $4$,所以在 $T_0$ 上 $7$ 的儿子就是 $6$ 和 $4$。
再见,DAG!
OI 中常用的 SAM 由 DAG 和 parent 树两部分组成。parent 树已经揉到基本子串结构里面了,所以现在我们尝试把 DAG 也搞进去。
以正串 SAM 为例,做一点粗分析:正串 SAM 的 DAG 表达的是“向 $r$ 增大的方向加字符时的转移”,在平面上其实就是“向上走”。如果某一行不在等价类的上边界,那么该行的点“向上走”就只能走到其上一行,于是 DAG 上这个结点就只会连出去一条边;反过来,如果某一行在等价类的上边界,那么该行上的点“向上走”的终点就会取决于这一行的点关联的 $T_1$ 的树边。
下面就来说明这样的现象。
首先,DAG 上转移时,已经在同一个结点内的字符串不会被拆开。我们需要说明树边转移,即“向左走”和“向上走”也满足这样的性质;下面这个引理就在做这个工作:
引理 3.2.5
如果 $s[l,r_1]$ 与 $s[l,r_2]$ 在同一等价类中,则 $\forall 1\le l'\le l$,$s[l',r_1]$ 与 $s[l',r_2]$ 在同一等价类中。
同理,如果 $s[l_1,r]$ 与 $s[l_2,r]$ 在同一等价类中,则 $\forall r\le r'\le |s|$,$s[l_1,r']$ 与 $s[l_2,r']$ 在同一等价类中。
证明
延续口胡证明的风格以拓展左侧为例。不妨设 $r_1\le r_2$,那么 $s[l,r_2]$ 包含 $s[l,r_1]$,所以 $s[l,r_2]$ 和 $s[l,r_1]$ 的出现位置可以建立一一对应关系。
那么,如果有 $s[p,p+r_1-l']=s[l',r_1]$,就有 $s[p+l-l',p+r_1-l']=s[l,r_1]$。根据一一对应关系,有 $s[p+l-l',p+r_2-l']=s[l,r_2]$。最后比对字符可以得到 $s[p,p+r_2-l']=s[l',r_2]$。所以 $\operatorname{occ}(s[l',r_1])\le \operatorname{occ}(s[l',r_2])$,可以结合引理 3.2.4导出二者在同一等价类中。
我们知道,DAG 上走字符为 $c$ 的转移边时,这个结点所代表的字符串都会在末尾加上 $c$。所以,我们还需要说明某一等价类的顶行处的 $T_1$ 树边可以被分成若干组,每一组边都需要满足:
顶行上的每个点都必须恰好关联该组内的一条边。
这些边指向同一个等价类的同一行。
顶行上横坐标之差为 $\delta$ 的两个点,关联的边指向的点的横坐标之差仍然为 $\delta$。这是因为同时加入一个字符后字符串相对长度不变。
可以证明满足这些限制的一组边就可以对应到 DAG 上的一条转移边。
下面这个定理就是在做这个工作。
定理 3.4
如果两个正串/反串 SAM 节点 $u,v$ 在同一个等价类中,那么这两个点在 parent 树上的子树除根节点外结构完全相同。
结构完全相同指可将子树内的点一一对应,使其作为无根树同构,且对应的点满足:包含的串的个数,$\operatorname{occ}$ 大小均相同。进一步的,对应的 SAM 节点在阶梯状网格图的相对位置(两行/列之间的距离)均与 $u,v$ 在阶梯状网格图的相对位置(两行/列之间的距离)相同。
证明
以正串 SAM 为例。在一个等价类中任取两行,记它们对应的 SAM 结点为 $u,v$。设 $b_u,b_v$ 分别为 $u,v$ 包含的最长的字符串。不妨设 $|b_u|\le |b_v|$。
因为 $u,v$ 同在一个等价类中,且一个等价类中的左边界对齐,所以 $\operatorname{posl}(b_u)=\operatorname{posl}(b_v)$。
设 $k=\operatorname{occ}(b_u),\delta=|b_v|-|b_u|$,则可以找出 $b_u$ 的出现位置按左端点升序排序为 $s[l_1,r_1],s[l_2,r_2],\dots,s[l_k,r_k]$,而 $b_v$ 为 $s[l_1,r_1+\delta],s[l_2,r_2+\delta],\dots,s[l_k,r_k+\delta]$。由引理 3.2.5,$\forall 1\le i\le k,1\le j\le l_k$,$s[j,r_i]$ 和 $s[j,r_i+\delta]$ 在同一等价类中,且在平面上的相对位置和 $b_u,b_v$ 的相对位置相同。我们就称“$s[j,r_i]$ 对应 $s[j,r_i+\delta]$”。
注意到,$u$ 子树中的串恰巧可以表示为 $\{s[j,r_i]:1\le i\le k,1\le j< l_i\}$,$v$ 子树同理。因此,这个对应关系可以使得 $u$ 子树内串的 trie 和 $v$ 子树内串的 trie 作为无根树同构,且对应的结点的 $\operatorname{occ}$ 相同。将 trie 的二度点缩掉就得到了 parent 树。
进一步地,刚刚的分组要求可以在下面这个推论中体现:
推论 3.2.4
可以把一个块的上边界连出的边分成若干组,每组会连向某个其他块一段连续且对齐的下边界。组数即 parent 树上的儿子个数。对于左边界同理。
Fig 3.5 树边分组示意图
现在在基本子串结构上,一行走 $T_1$ 树边的整体转移与在 DAG 上走一条字符边的性质无异,我们只需要按照字符对应起来。根据推论 3.2.4,我们只需要随便取出一行上的一个点出来,将它在 $T_1$ 上的树边和 DAG 上的字符边对应起来即可。
于是,我们得到:
引理 3.2.6
对于一个 $T_0$ 上的点,如果其不对应其所在块的上边界,那么它在 SAM 上有且仅有一条出边,连向它上面的行所对应的节点;如果其对应的是上边界,则它的所有出边即连向从该上边界用另一棵 SAM 的 parent 树边连出能到的所有下边界表示的 SAM 节点。
对于 $T_1$ 上的点类似。
这样,我们就将 DAG 的结构完全用另一个 SAM 的 parent 树替代了。
3.3 构建
光说无益,没有构建算法的话基本子串结构就还是空中楼阁。
细想一下,要构建基本子串结构,我们只需要做好几件事——首先构建 SAM,其次识别代表元并初步确定等价类,然后划分等价类,最后按顺序安放行和列。
令 $n=|s|$。以下是详细过程:
构建正反 SAM
众所周知,SAM 可以在 $O(n)$ 时间内完成构建。
以下就称正串 SAM 为“正 SAM”,反串 SAM 为“反 SAM”。
识别代表元
根据引理 3.2.6,我们只需要识别出来正反 SAM 哪些结点包含等价类的代表元即可。
注意到,代表元必然是一个 SAM 结点包含的最长的字符串。因此,我们可以考虑“枚举”正 SAM 上每一个结点的最长字符串。同时注意到,根据平面上点的分布规律,正 SAM 上一个结点的最长字符串必然落在同一列(等价类的左边界)上;而其中,代表元又是该列最长的那个字符串。因此,如果我们可以对于正 SAM 的每一个结点,找到其最长字符串所在的反 SAM 结点,就可以通过比较长度,知道该字符串是否为代表元。顺便,我们还完成了“将两个 SAM 的等价类对应起来”的工作。
按 论文中判断是否为等价类边界的方法为“检查自动机上的出边”,对应等价类的方法为“找到代表元的 $\operatorname{posl}$ 和 $\operatorname{posr}$”。正确性不必多说,但是似乎很难保证线性复杂度?
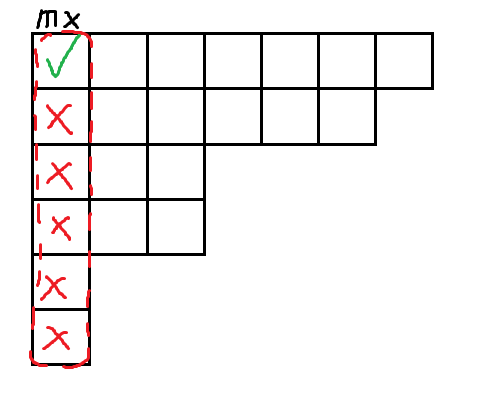
具体到实现,我们可以对于正 SAM 的 DAG 做 DFS 或 BFS,每次只沿着 $\text {mx}_v=\text{mx}_u+1$ 的弧 $u\rightarrow v$ 进行转移。同时,在反 SAM 上维护当前走过的路径代表的字符串所在的结点。因为是一直在向后加字符,所以反 SAM 上一直走的是树边。为了处理这个过程,需要提前预处理反 SAM 上各个字符转移到的儿子。这样就是 $O(n)$ 的。
如果对于复杂度要求不高的话,在反 SAM 上找对应时则可以“先在原串上定位区间,再在反 SAM 的 parent 树上树上倍增”解决,复杂度变为 $O(n\log n)$。
划分等价类
现在我们只需要确定不包含代表元的结点所在的等价类编号即可。
根据引理 3.2.6,这些结点在 DAG 上必然只有一条出边。现在我们需要一个正确的编号顺序,使得给某个未划分结点确定等价类时,其出边指向的结点已经被确定了等价类,那么毫无疑问按照 $\text{mx}$ 从大到小扫描即可。
实际实现时,按照 SAM 的结点编号倒着扫描也是一个合理的顺序,原因暂时未知。
排序行列
把行列放到等价类里面已经不是问题,现在我们需要将它们排序。具体来说,行应当按照 $r$ 有序,而列应该按照 $l$ 有序。“但其天然与 SAM 构建时加入的顺序相同”,故可以直接按照 SAM 的编号将行列放到等价类里面。
具体什么原理搬运人也不是很清楚。可能是因为 SAM 增量构建的过程中,同一等价类内部的行和列都是有序出现的吧。
至此,一个完整的基本子串结构就已经建立了。上面介绍的是一个离线的 $O(n)$ 的算法,实现并不复杂;同时也存在更加简单粗暴的 $O(n\log n)$ 算法。
至于在线构建算法,论文之中没有提到,搬运人也不会,故还有待探索!
3.4 应用
我们将通过论文例题和其他题目简单展示一下基本子串结构的应用。
因为这个结构还比较新,所以相关应用可能还不是很多。
例题 3.1.1
题目见前文。
解法
知道了结点,自然就可以知道它们所在的等价类和它们对应的行和列。
如果它们不在同一个等价类,则交集显然为空。如果在一个等价类中,则交集为行列包含的点的交集。
下面这个例题是比较新的,通过它可以一窥基本子串结构的强大。
例题 3.4.1(「CF1817F」Entangled Substrings)
给定一个字符串 $s$,你需要求出有多少个字符串有序对 $(a,b)$ 满足:
$a,b$ 都是 $s$ 的非空子串。
存在一个可为空的字符串 $c$ 使得:
若 $s[l,r]=a$,则 $s[l,r+|c|+|b|]=acb$。
若 $s[l,r]=b$,则 $s[l-|c|-|a|,r]=acb$。
也即,$a,b$ 仅会在 $acb$ 这样的子串中出现。
解法
很显然,题目条件就是 $a,b$ 要和 $acb$ 在同一个等价类中。
假设我们已知 $acb$ 对应的点,坐标为 $(l_0,r_0)$,那么 $a$ 的坐标一定是形如 $(l_0,r)$,$b$ 的坐标一定是形如 $(l,r_0)$。同时,因为 $a,b$ 要在同一个等价类中,所以还应该存在边界 $r_a,l_b$,以限制 $r_a\le r\le r_0,l_0\le l\le l_b$。
根据坐标的性质,一定有 $r_a\ge l_0,l_b\le r_0$。注意到合法的 $acb$ 还应该满足 $r
我们可以枚举 $r_a$,这样可行的 $l_b$ 对应于行的前缀(从上到下)。此时计算只需要知道 $\sum l_b^2,\sum l_b,\sum 1$,所以维护好这几个和就可以了。阶梯状图形自带的单调性使得我们可以双指针 $O(n)$ 解决本题。
参考代码。
基本子串结构也可以完成某些 SAM 变种可以完成任务。下面这个例题原本的解法需要用到对称压缩 SAM,但是利用好基本子串结构解决它也并不困难:
例题 3.4.2(「UOJ577」打击复读)
给定长度为 $n$ 的字符串 $s$,第 $i$ 个字符有两个权值:左权值 $wl_i$ 和右权值 $wr_i$。定义一个子串 $s[l, r]$ 的左权值 $vl(s[l, r])$ 为:其在原串中各个出现位置的左端点的左权值 $wl$ 和;右权值 $vr(s[l, r])$ 为:其在原串中各个出现位置的右端点的右权值 $wr$ 和。定义一个子串 $s[l, r]$ 的复读程度是它的左权值与右权值的乘积,即 $w(s[l, r]) = vl(s[l, r])\cdot vr(s[l, r])$。
s 的复读程度定义为所有子串复读程度的和,即:
$$ \sum_{i=1}^{|S|}\sum_{j=i}^{|S|}w(s[i,j]) $$
$q$ 次修改某个 $wl_i$ ,查询整串的复读程度,对 $2^{64}$ 取模。
解法
注意到,整串的复读程度一定可以被表示为 $wl$ 的线性组合,所以求出各个 $wl$ 的系数就可以 $O(q)$ 解决所有询问。
首先将原串的正反 SAM 建出来。那么,对于一个子串 $t$ 而言,$vr(t)$ 仅仅和其所在的正 SAM 结点(即 $T_0$ 结点)有关,$vl(t)$ 仅仅和其所在的反 SAM 结点(即 $T_1$ 结点)有关。而 $T_0$ 结点对应的 $vr$ 和 $T_1$ 结点对应的 $vl$ 其实都是子树和。
将这个问题放到基本子串结构上,则相当于等价类的每一行有一个权值 $vr$,每一列有一个权值 $vl$,$t$ 的权值就是所在行列的权值的乘积。会和某一个 $vl$ 乘起来的 $vr$ 一定是一段行的前缀(从上到下),所以滚一个前缀和即可知道 $vl$ 的系数。再将 $vl$ 的系数反着推到 $wl$ 上就得到了 $wl$ 的系数。
时间复杂度为 $O(n+q)$。参考代码。
值得一提的是,根据论文的说法,对称压缩 SAM 实际上就是将每个等价类压缩成了一个结点,两棵 parent 树的边就形成了两个方向的自动机的结构。
处理子串的子串的信息时,基本子串结构告诉我们,你实际上就是在做一个二维数点:
例题 3.4.3(「UOJ697」广为人知题)
给定一个长度为 $n$ 的字符串 $s$,字符集为小写英文字母。
给定 $m$ 个模式串,第 $i$ 个为 $s[\mathrm{tl}_i \cdots \mathrm{tr}_i]$($s$ 的下标从 $1$ 开始)。
现有 $q$ 次查询,每次给出 $[\mathrm{ql}_i, \mathrm{qr}_i]$,求所有模式串在 $s[\mathrm{ql}_i \cdots \mathrm{qr}_i]$ 中的出现次数之和。
解法
(和论文的做法有出入,但是本质相同)
考虑对于每一个模式串,在平面上将它的出现位置对应的点的权值全部 $+1$。那么,一次询问就是在 $\{(x,y):x\ge \mathrm{ql},y\le \mathrm{qr}\}$ 的范围内求点的权值和。
注意到询问的答案和 $s[\mathrm {ql},\mathrm {qr}]$ 所在的位置无关,所以我们可以去掉它的位置,转而在 $s[\mathrm {ql},\mathrm {qr}]$ 所在的等价类里面考虑这个询问。
考虑将贡献分为“与 $(\mathrm{ql},\mathrm{qr})$ 同在一个等价类的”和“在 $(\mathrm{ql},\mathrm{qr})$ 所在等价类之外的”。前者因为总共点数为 $O(m)$,所以可以直接二维数点解决。
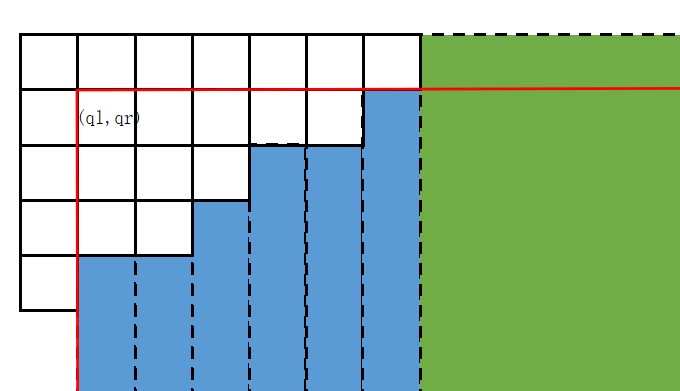
第二种贡献则需要对于等价类之外的区域划分。首先按照列划分,如下图所示:
Fig 3.7 平面划分 等价类中若有 $c$ 列,则将前 $c$ 列单独划分出来(蓝色区域);右侧则会剩一块区域没有被等价类的列覆盖到,可以将它们全部划分为一块(绿色区域)。
蓝色区域对应的是 $T_1$ 上祖先包含的权值之和,可以预处理;绿色区域则为另一个等价类的代表元进行询问得到的结果,也可以提前处理出来。
此时就可以算出 $\{(x,y):x\ge \mathrm{ql}\}$ 部分的答案。而减去 $\{(x,y):x\ge \mathrm{ql},y>\mathrm {qr}\}$ 就相当于减去行的前缀的右侧部分,对应的是每一行 $T_0$ 上祖先包含权值之和的前缀和,仍然可以预处理。
此外,定位子串所在等价类的复杂度为 $O((m+q)\log n)$,于是我们就得到了一个 $O(n+(m+q)\log n)$ 的做法。
参考代码,
但是我写的常数太大了,跑不过 $\log^2n$。
最后看一眼 SDOI2022 吧家人们:
例题 3.4.4(「SDOI2022/SXOI2022」子串统计)
给定长度为 $n$ 的字符串 $s$。令 $T_0 = s$。每次删除 $T_i$ 的开头或结尾的字符,得到新的字符串 $T_{i+1}$,经过 $n − 1$ 次操作之后,会得到只有一个字符的串 $T_{n−1}$。根据每次删除的选择,一共有 $2^{n−1}$ 种可能的操作序列。
对于一个操作序列,记其权值为:
$$ \prod_{i=1}^{n-1} \operatorname{occ}_s(T_i) $$
求出所有操作序列的权值和,对 $998244353$ 取模。
解法
一个操作序列实际上是“从平面上 $(1,n)$ 出发,每次只能向下或向右走,走到任意一个 $(x,x)$"的一条路径。它的权值几乎就是经过的每个结点的 $\operatorname{occ}$ 之和。
注意到,一个等价类中的 $\operatorname{occ}$ 全部相同,因此可以想到将一个等价类中的放到一起转移。为了计算的方便,计算时反着考虑路径,也就是从 $(x,x)$ 推到 $(1,n)$。
在一个等价类中,假设阶梯状边界上的点所在行列为 $(a_1,b_1),(a_2,b_2),\dots,(a_m,b_m)$,到各个点的权值和为 $f_1,f_2,\dots,f_m$,则贡献到第一行的 OGF 形如 $\sum_{i=1}^m\frac{x^{a_i}\cdot f_i\operatorname{occ}^{b_i}}{(1-\operatorname{occ}x)^{b_i+1}}$。因为 $a,b$ 同调,所以可以分治算出这个分式。
一个等价类的复杂度为 $O(\operatorname{per}(a)\log^2n)$,总复杂度即为 $O(n\log^2n)$。
没有参考代码......
4 基本子串结构上的树链剖分
咕且姑着。

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号